卫星变轨问题

从仰望星空到探索星海，人类从未停止对宇宙的向往. 太空中，数以千计的人造卫星如同精密钟表，在各目的轨道上运行，构成现代社会的“神经中枢”. 然而这些卫星并非自发射起就固守一方.

它们如何从一条轨道跃迁至另一条？

如何实现与空间站的“万里穿针”？

这背后的答案，都指向航天动力学的核心问题——卫星变轨. 它是一场引力、速度与轨道能量精心编排的“宇宙之舞”，是人类智慧将牛顿与开普勒定律应用于星辰大海的完美体现.

我们都知道之所以人造卫星围绕着地球做匀速圆周运动，是因为地球作用在人造卫星上的引力充当了向心力，并且人造卫星在其轨迹切线方向上所受外力合力为零. 那么你有没有想过当人造卫星想要迁移到离地面更高的轨道运行时候，应该运用什么物理原理呢？

• 下图是一张示意图作为辅助：设当人造卫星在半径为 r₁ 的轨道三上做原速圆周运动时，其周期为T₁. 当人造卫星通过点 A 时， 启动切向推动器，这时候人造卫星切向速度从 v₁ 增加到 v₂， 这时候人造卫星将沿着椭圆轨道绕地球运动，即轨道二.

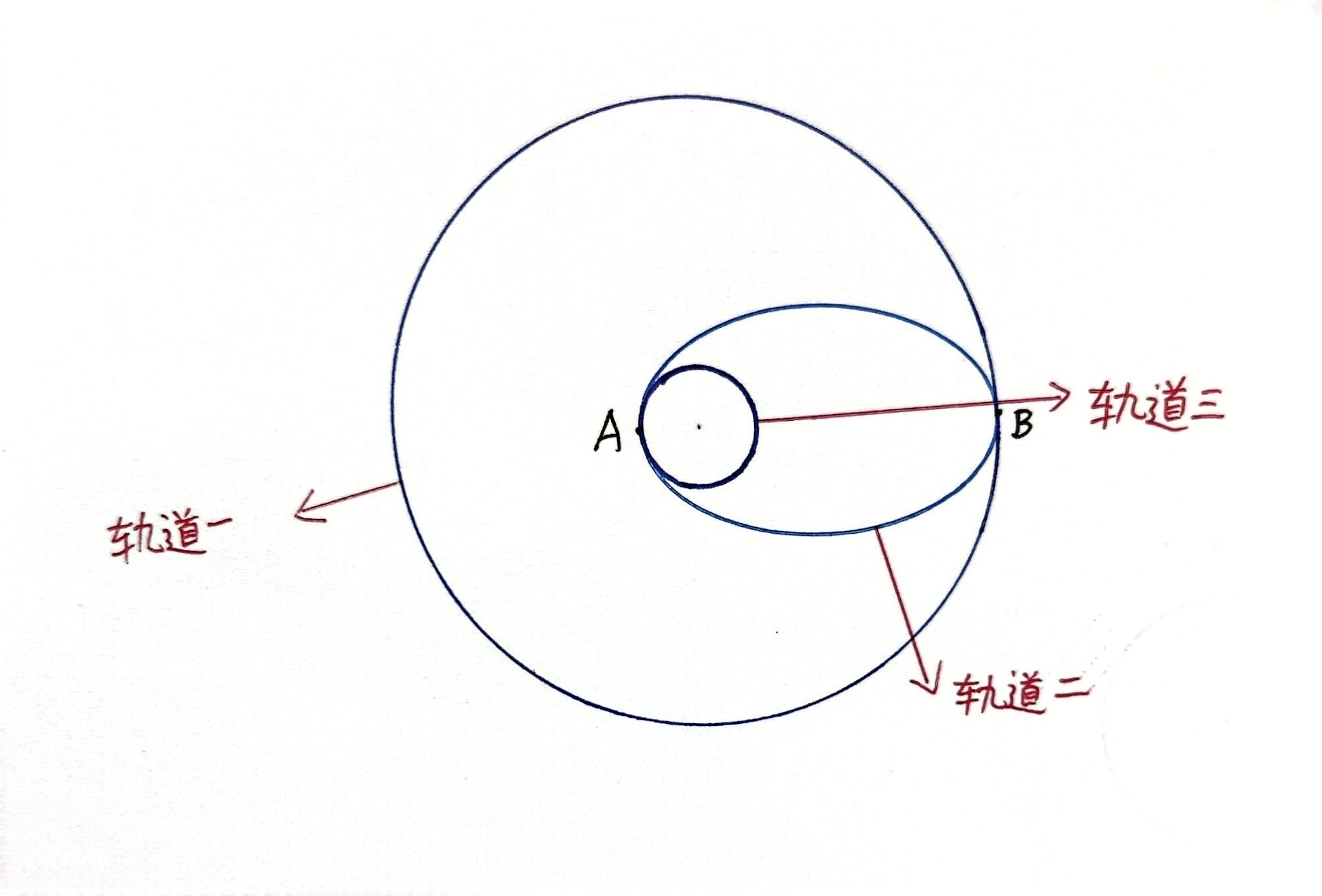
为什么会沿着椭圆轨道运动呢？

数学上（由开普勒第一定律和牛顿力学证明），在所有平方反比引力（如万有引力）的系统中，一个具有特定能量（比圆轨道能量高，但比逃逸能量低）的物体，其稳定运行的轨道就是一个椭圆，而引力中心（地心）则位于这个椭圆的一个焦点上. 当人造卫星在 B 点加速，使其速度达到该处圆轨道运行所需的速度 v₃ 时，人造卫星会沿着半径为 r₂ 的轨道一做匀速圆周运动，因为此时地球作用在人造卫星上的引力再次充当向心力.

如何求人造卫星从轨道三变轨至轨道一的时间 t 呢？

计算过程请见下图：其中 a 表示椭圆轨道的半长轴长度，T₂ 表示人造卫星沿椭圆轨道（轨道二）运行的周期，k是常数.

这里很多小伙伴会疑惑什么是开普勒第三定律，这里小编给大家科普一下开普勒三大定律的定义：

第一定律：轨道定律

定义：所有行星绕太阳运动的轨道都是椭圆，太阳位于这个椭圆的一个焦点上.

第二定律：面积定律

定义：在相等的时间内，行星与太阳的连线扫过的面积相等.

第三定律：周期定律

定义：所有行星轨道半长轴的立方与其公转周期的平方之比是一个常数.

总而言之，开普勒定律不仅解释了天体的自然运行，更构成了人类主动规划和控制航天器轨道、实现星际穿越的理论蓝图.